Introduction

Potential of Biomechanical Properties: Pathological changes in tissues provide important diagnostic information. Bulk modulus is an intrinsic mechanical characteristic of materials and can be measured by ultrasound as the speed of sound.
Limitations of Current Ultrasound Imaging: While B-mode ultrasound is valuable for detecting breast cancer, it struggles with specificity in differentiating benign from malignant tumors. This leads to unnecessary biopsies, and its interpretation is highly dependent on the operator’s skill.
Clinical limitations of using Ultrasound Computed Tomography (USCT) : While USCT can reconstruct SoS using multiple transducer elements, it requires bulky setups and submerging the body part in a water tank, limiting its clinical use outside the breast.
The aim of this paper is to present a method of quantitative SoS imaging using conventional ultrasound probes.

Principle : Jaeger et al, 2015.

Considering straight ray approximation, the slowness can be directly linked to the differential time-of-flight based on apparent displacements along different ultrasound wave propagation paths when changing the steering angle.

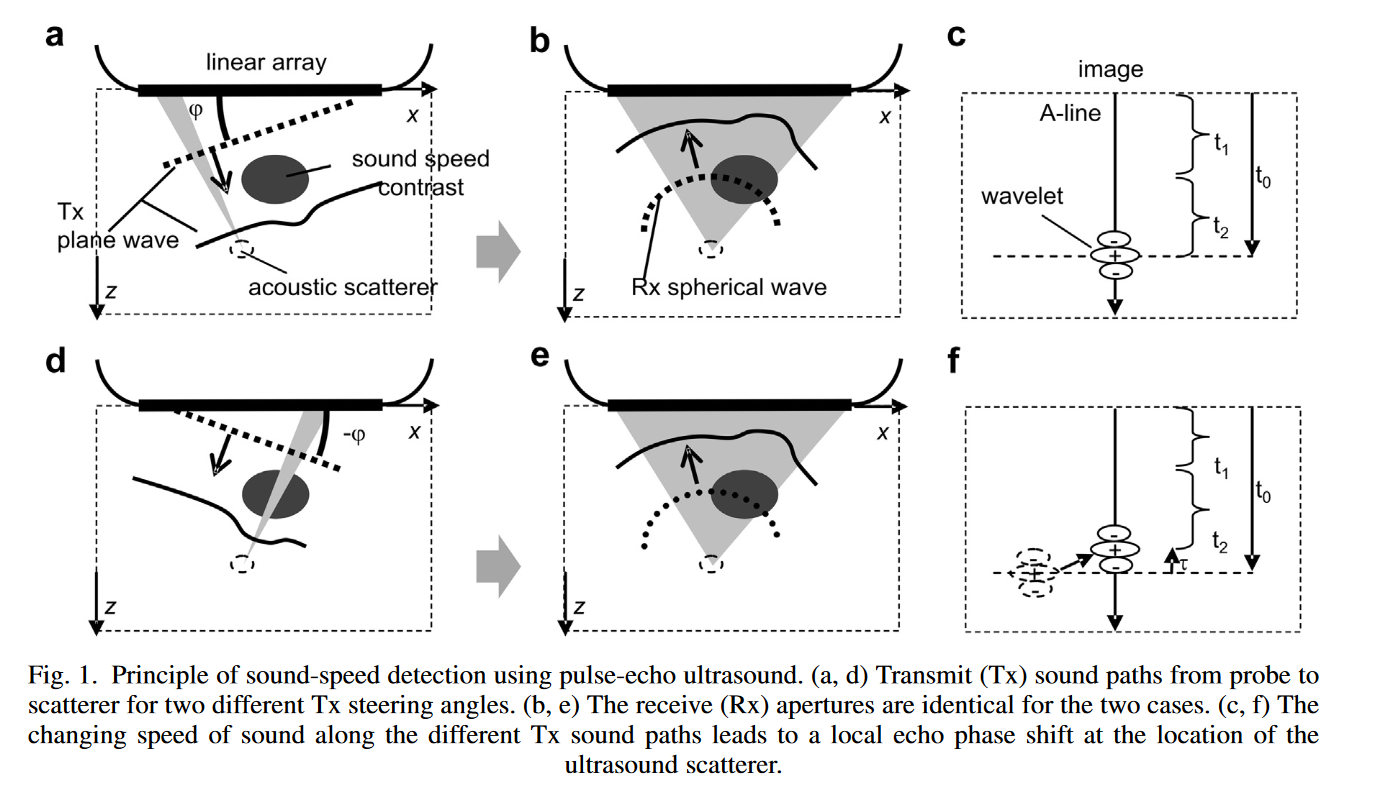
The transmitted (Tx) wave reaches the hypothetical scatterer after traveling along the path shown by the gray wedge, which is unaffected by the contrast region. However, this changes when the Tx angle shifts from $\Phi$ to -$\Phi$. In this case, the portion of the Tx wave that reaches the scatterer passes through the contrast region, causing it to arrive at the scatterer earlier than it would in the hypothetical scenario where there is no sound-speed contrast. This results in a shorter t1. Since the reception is performed on all elements, the reception time wouldn’t be influenced if changing the steering angle. The transmission time can therefore be written as : $T(\theta) = T_0(\theta) + \tau(\theta)$.

Problem formulation in spatial domain

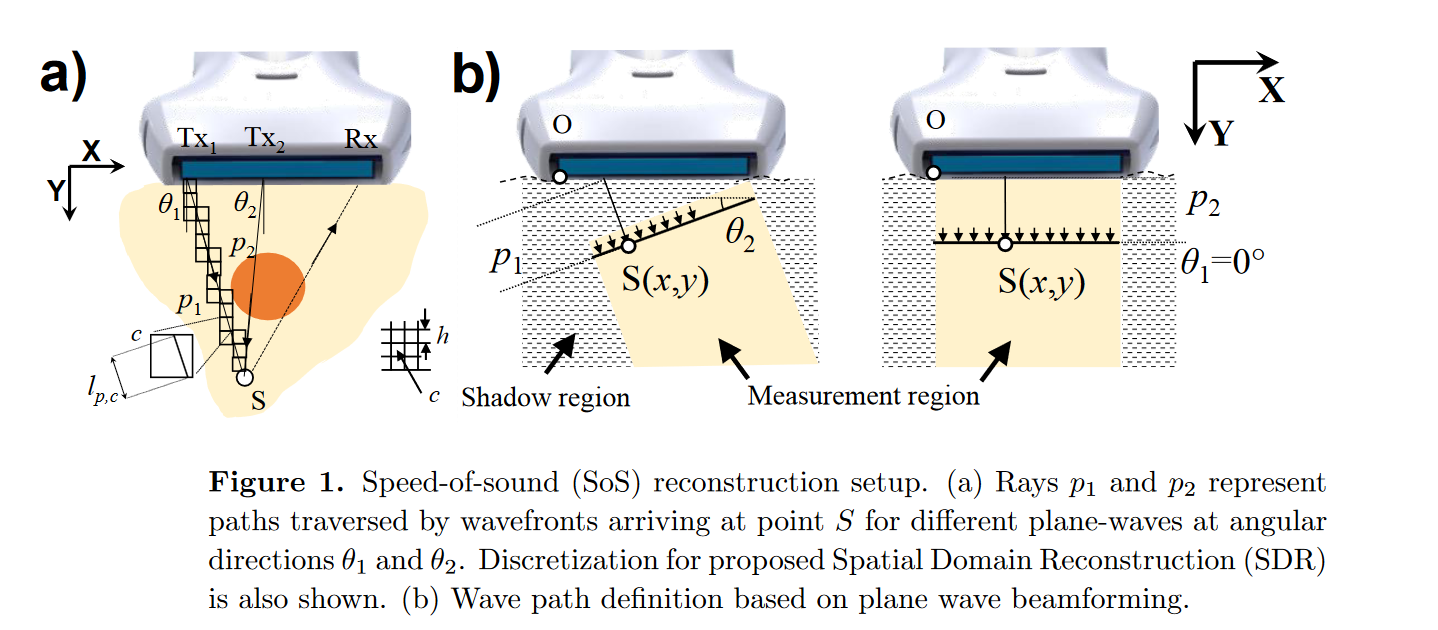
Spatial domain discretization to a 2D grid containing a finite number of cells C.
Considering the path length lp,c per ray path and cell c, the time of flight can be linked to the slowness as follows :

\[t_p = \sum l_{p,c} \sigma _c\]

Considering two ray paths with different steering angles, the sound speed deviations accumulated along the propagation paths can manifest in a shift in the time of flight :

\[\begin{aligned} \tau_m &= \sum_{c=1}^{C} \left( \sum_{p=1}^{P} w_{m,p} l_{p,c} \right) \\ &= \sum_{c=1}^{C} L_{m,c} \sigma_c \end{aligned}\]

The forward problem is hence :

\[\tau = L \sigma\]

In pulse-echo imaging using a conventional ultrasound probe with single-sided tissue access, each cell is only affected by a restricted range of angular directions (θ1, θ2, …), making the reconstruction problem incomplete. Moreover, the presence of shadow regions lead to an ill-conditioned sparse matrix L. => The problem needs to be solved as a regularized optimization problem :

\[\hat{\sigma} = \arg\min_{\sigma} \|\boldsymbol{\tau} - \mathbf{L} \boldsymbol{\sigma} \|_1 + \lambda \|\mathbf{D} \boldsymbol{\sigma} \|_1,\]

Considering limited-angle nature of the USCT problem, i.e., with naturally lower resolution in the axial direction, one can regularize gradients in each axis differently. In this paper, they used Multi-Angle Anisotropically-Weighted Total Variation which is based on considering multiple gradient directions in the spatial regularization term, rather than using just two orthogonal gradient estimates.

\[\hat{\sigma}_{\text{MA-AWTV}} = \arg\min_{\sigma} \|\boldsymbol{\tau} - \mathbf{L} \boldsymbol{\sigma} \|_1 + \lambda \sum_{i,j} \sum_{\alpha} \kappa_{\alpha} | D_{\alpha} \boldsymbol{\sigma} |,\]

Bayesian approach : Incorporation of prior known data from B-mode imaging to reduce the number of degrees of freedom in the reconstruction of the inverse problem.

The quantitative speed of sound maps are then derivated from the slowness as SoS =$\sigma ^{-1}$

Multiple plane-wave transmits for a practical imaging scenario

Plane wave Tx and focused Rx beamforming.
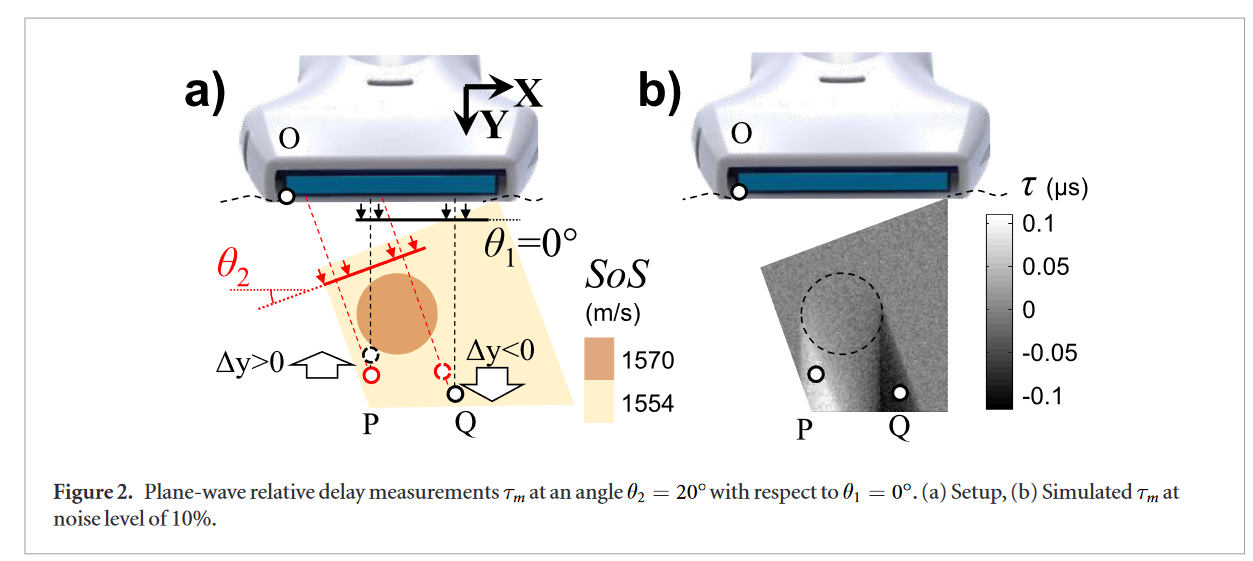
ToF shifts are measured through the registration of 2 B mode images acquired at 2 different steering angles using a zero-normalized crosscorrelation to find the vertical displacement $\Delta y$: $\tau = \Delta y / v / cos(\theta)$

Experiments and results

A typical MA-AWTV reconstruction in CVX presently runs in less than 30 s on an Intel R© CoreTM i7-4770k CPU @3.5 GHz with 16 GB RAM for a single frame and for a domain of size 40 × 38 mm with 0.3 mm reconstruction discretization using a pair of plane-wave angular projections with the same discretization resolution.

Using synthetic data, the study focused on investigating the effect of :

Noise by artificially introducing gaussian noise.
Regularization method (L2 regularization / TV / L2-data AWTV / AWTV / MA-AWTV).
Parametrization $\lambda$
Number of steering angles

Established a comparison between fourier domain problem formulation and spatial domain problem formulation.

Frequency-versus spatial-domain reconstruction

$\tau$ values per each cell c were directly generated using ray tracing for calculating L and the same geometric weights L were used in the inverse problem.

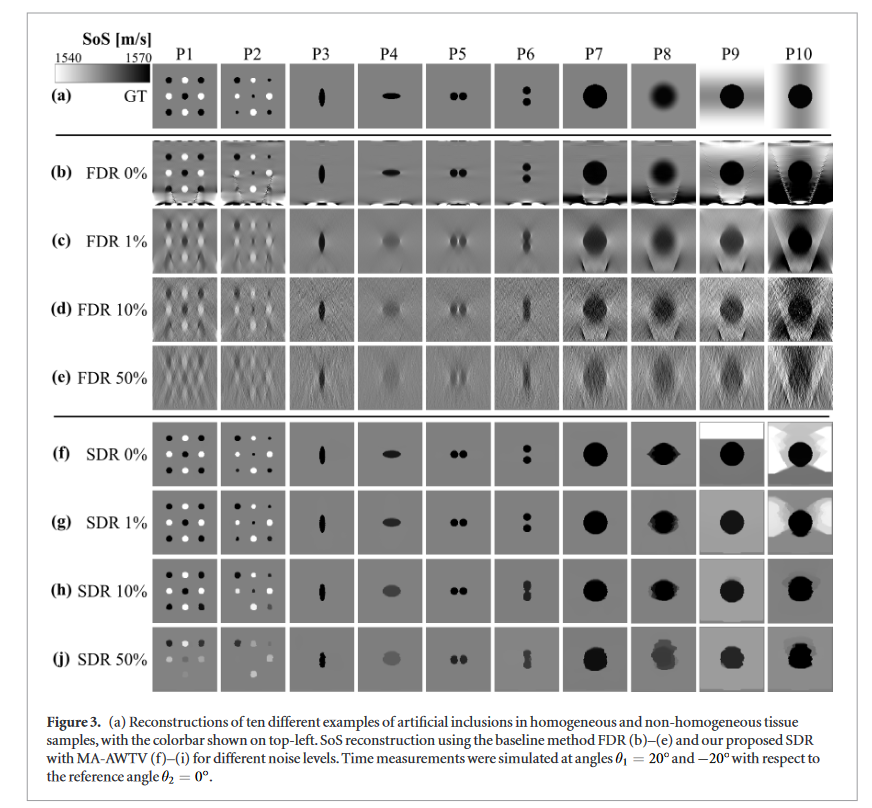The proposed SDR method provides a visible image quality improvement with respect to FDR.

The SDR method achieves piecewise delineation of homogeneous inclusions, effectively filtering out noise from the images.

Regularization norm

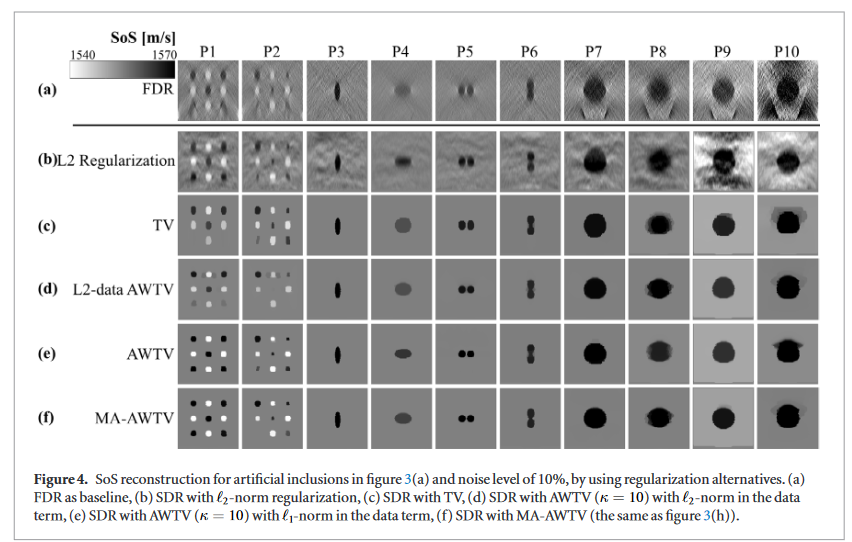The proposed SDR is superior to FDR regardless of the data and regularization norm.

The use of multiple regularization directions with MA-AWTV improves the reconstruction for edges that are not axis-aligned.

Parametrization

SDR is observed to be robust against variations in the regularization constant λ.

λ = 0.025 was found be give fair reconstruction regardless the inclusion geometries and noise levels.

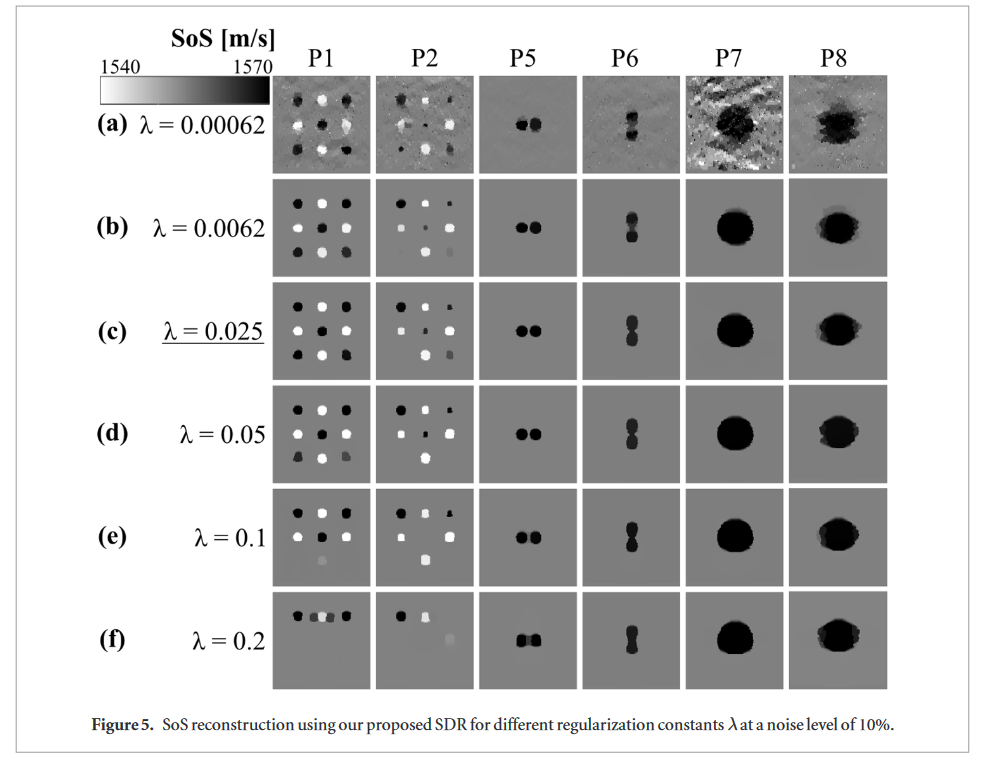
Too small λ (e.g. λ = 0.00062) introduces noise in the images, whereas too large λ lead to over-regularization, which smears the inclusion geometries.

Multi-angle reconstruction

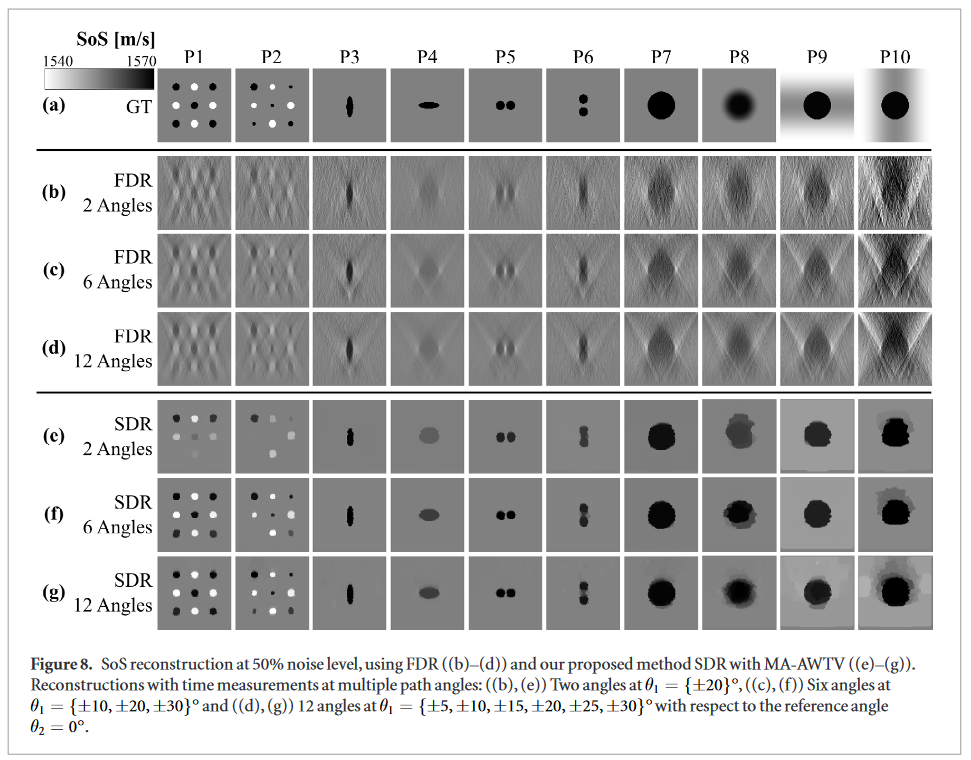SDR results significantly improve with increasing number of plane-wave angles. For instance, smaller inclusions are resolved in examples P1 and P2, and the vertical inclusions in P6 are separated.

Numerical wave simulations

As a more realistic simulation,they performed numerical simulations of wave propagation. A tissue domain of size 45 mm × 40 mm was simulated, where an inclusion of 5 mm radius was located at the depth of 20 mm. The inclusion had a speed-of-sound of 1548 m/s and the background 1515 m/s, which simulated a tumor with 2.2% speed-of-sound contrast. The sampling frequency of the transducer was set to 5 MHz.

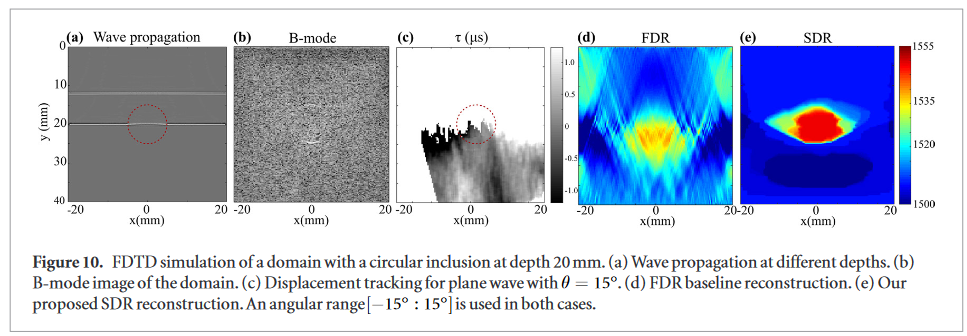
In vivo data

Data was recorded from a female patient (of 80–90 year-old age group) with a breast lesion, which the biopsy later revealed as invasive ductal carcinoma.

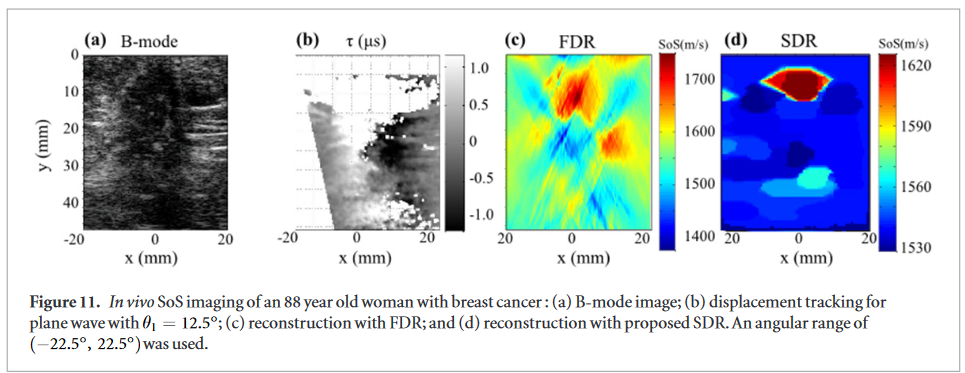
SDR algorithm delineates an inclusion geometry at (x = 0, y = 10) above the mid-range SoS value (1580 m/s), as a single focal region as confirmed by biopsy and with a lateral extent in agreement with that observed in B-mode.

Conclusions

The numerical experiments demonstrate that the proposed SDR ( spatial domain reconstruction) method enables precise reconstruction of sound speed maps with excellent spatial resolution and contrast compared to FDR (frequency domain reconstruction) formulation.
SDR formulation can exclude regions of missing information in the reconstruction.
The technique is sensitive to low variations in speed of sound.

Limitations and further studies :

Neglecting ray trajectory variations due to physical effects such as refraction, diffraction and interference effects.
Compare different speckle tracking techniques.
Extensions are envisaged to obtain other acoustic parameters such as the attenuation coefficient.
Apply the method to other probe geometries.